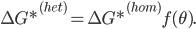Neste Tópico, prosseguimos o desenvolvimento proposto no tópico anterior (Tópico 15.7). A barreira energética associada à formação de um núcleo de tamanho crítico, com formato de calota esférica, por nucleação heterogênea sobre a parede do molde, será fornecida pela expressão:
(15.17)
onde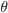 
é o ângulo de molhamento. Por sua vez, 
é um fator de forma cuja expressão é:
(15.18)
A Equação (15.18) mostra que a barreira energética para a nucleação sobre um substrato decresce com o decréscimo de 
e que se aproxima de zero à medida que 
se aproxima de zero. Para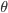 
= 0°, teoricamente não existe barreira energética a ser superada para a nucleação sobre um substrato. Assim, mesmo numa situação em que o número de sítios possíveis para a nucleação heterogênea seja pequeno, as partículas se formarão preferencialmente nas superfícies ao invés de nuclearem-se no interior do líquido. A Figura 15.j mostra graficamente o fator 
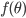que converte a barreira energética para a nucleação homogênea em heterogênea, em função do ângulo 
. Pode ser visto que, mesmo para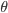 
= 90°, que representa o limite de aplicação da Eq. (15.18), o fator 
ainda é igual a 
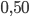. Isto significa que, mesmo para um líquido que molha parcialmente o substrato, a energia necessária para nucleação heterogênea ainda é metade do valor da energia necessária para a nucleação homogênea. Para um líquido que molha muito o substrato (
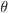pequeno), por exemplo 30°, o quociente da Figura 15.j vale 0,02. Portanto, a energia para a nucleação heterogênea é 50 vezes menor do que para a homogênea.
A curva de velocidade de nucleação heterogênea deve se assemelhar à da Figura 15.e (veja Tópico 15.5), exceto pelo fato de que a nucleação heterogênea pode iniciar-se em temperaturas muito mais altas que aquelas previstas para o caso da nucleação homogênea. A nucleação heterogênea reduz e, algumas vezes, elimina o super-resfriamento. Para condições de estado estacionário, a velocidade de nucleação heterogênea pode ser expressa como:
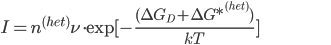(15.19)
em que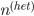 
é o número de átomos (ou moléculas) na fase líquida, por unidade de área, em contato com a parede do molde, 
é a freqüência de salto, 
é a energia de ativação para difusão, k é a constante de Boltzmann, T é a temperatura absoluta (K) e 
é a energia de ativação para o processo de nucleação heterogênea. A Figura 15.k é uma animação do crescimento heterogêneo de uma nova fase a partir de uma fase gasosa.
Figura 15.j – Variação da razão entre as barreiras energéticas para a nucleação heterogênea e para a homogênea em função de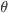 
.
Figura 15.k – Crescimento heterogêneo de uma nova fase a partir de uma fase gasosa. Observar a alteração na geometria da nova fase (de placa bidimensional para uma calota esférica tridimensional) em função do valor da força motriz do processo 