Em sistemas condensados, como é o caso do surgimento de uma fase sólida no interior de outra fase sólida, produzem-se variações de volume e deformações, cuja energia deve ser levada em conta.
Considere-se um sistema em que apenas uma fase 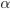 é estável acima da temperatura
é estável acima da temperatura 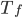 e que, abaixo de
e que, abaixo de 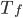 , duas fases (
, duas fases ( e
e 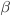 ) são agora estáveis. A variação total de energia livre, associada à formação – por nucleação homogênea – de um precipitado esférico de
) são agora estáveis. A variação total de energia livre, associada à formação – por nucleação homogênea – de um precipitado esférico de 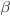 em matriz
em matriz  ,
, 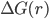 , é:
, é:
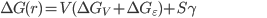 (15.12)
(15.12)
em que 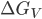 é a variação da energia livre por unidade de volume que resulta na formação da partícula de raio r,
é a variação da energia livre por unidade de volume que resulta na formação da partícula de raio r, 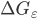 é a variação na energia de deformação do reticulado e
é a variação na energia de deformação do reticulado e 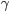 é a energia superficial. Como a partícula é esférica e de raio r, tem-se que
é a energia superficial. Como a partícula é esférica e de raio r, tem-se que 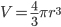 e
e 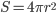 .
.
Os valores do raio do núcleo esférico sólido de tamanho crítico,  , e da barreira energética associada à formação do núcleo de tamanho crítico,
, e da barreira energética associada à formação do núcleo de tamanho crítico, 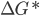 , podem ser obtidos pelas expressões:
, podem ser obtidos pelas expressões:
 (15.13)
(15.13)
e
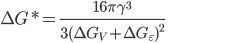 (15.14)
(15.14)
Quando existe um perfeito ajuste entre os planos e direções cristalográficas, através da interface que separa a partícula nucleada e a matriz, tem-se uma interface coerente ou uma partícula coerente. Como exemplo deste tipo de interface pode ser citado o contorno de grão de pequeno ângulo (1). Como a energia total de deformação associada à partícula tende a crescer com o seu tamanho, a partícula pode perder a sua coerência. Um exemplo deste tipo de interface é o contorno de grão de alto ângulo. A Figura 15.f apresenta um diagrama esquemático, mostrando contornos de grão de baixo e alto ângulos.
No caso da interface coerente, a energia de deformação da partícula não é muito dependente de seu formato, mas, no caso da interface incoerente, a forma da partícula pode ser muito importante, conforme mostra a Figura 15.g(2). Nesta figura o precipitado é considerado como elipsóide de revolução, com semi-eixos  e
e  .
.
Devido às restrições impostas, a velocidade de nucleação  será muito menor, se comparada com a transformação líquido-sólido. De fato, as transformações de fase no sólido ocorrem com velocidades de nucleação muito pequenas ou desprezíveis (para efeitos práticos), perto de
será muito menor, se comparada com a transformação líquido-sólido. De fato, as transformações de fase no sólido ocorrem com velocidades de nucleação muito pequenas ou desprezíveis (para efeitos práticos), perto de 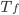 , sendo necessário um super-resfriamento (veja Tabela 15.1 no Tópico anterior) a fim de se aumentar a velocidade da transformação.
, sendo necessário um super-resfriamento (veja Tabela 15.1 no Tópico anterior) a fim de se aumentar a velocidade da transformação.
Figura 15.f – Diagrama esquemático mostrando contornos de grão de baixo e alto ângulos.
Figura 15.g – Energia de deformação relativa de uma partícula incoerente como função de sua forma.