Os desenvolvimentos mostrados a seguir permitem a obtenção das equações para o raio crítico 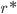 da uma fase sólida que surge dentro do líquido, e a energia de ativação
da uma fase sólida que surge dentro do líquido, e a energia de ativação  necessária para que este volume sólido seja formado.
necessária para que este volume sólido seja formado.
Para a nucleação de uma fase condensada,  pode ser obtido a partir da definição de Energia Livre de Gibbs:
pode ser obtido a partir da definição de Energia Livre de Gibbs: 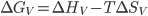 . No ponto de solidificação (ou seja, quando
. No ponto de solidificação (ou seja, quando  ) tem-se que
) tem-se que 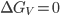 . Portanto:
. Portanto:
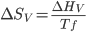 . (15.5)
. (15.5)
Pode-se, então, escrever:
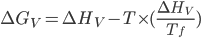 .
.
 .
.
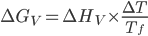 . (15.6)
. (15.6)
A Eq. (15.6) é uma boa aproximação para temperaturas próximas de 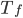 . Nesta expressão,
. Nesta expressão, 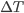 representa o grau de super-resfriamento
representa o grau de super-resfriamento ;
; 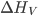 é o calor de fusão por unidade de volume (1). Substituindo nas Eqs. (15.3) e (15.4) o valor de
é o calor de fusão por unidade de volume (1). Substituindo nas Eqs. (15.3) e (15.4) o valor de 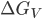 dado na Eq. (15.6), tem-se:
dado na Eq. (15.6), tem-se:
 . (15.7)
. (15.7)
e
 . (15.8)
. (15.8)
A Figura 15.c apresenta a variação de 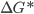 e
e 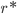 com a temperatura, com base nas Eqs. (15.7) e (15.8).
com a temperatura, com base nas Eqs. (15.7) e (15.8).
O valor de 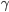 é relativamente insensível à temperatura, ao passo que
é relativamente insensível à temperatura, ao passo que 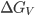 aumenta muito o seu valor negativo à medida que a temperatura é reduzida. As Eqs. (15.7) e (15.8) indicam que não somente o raio crítico diminui com o aumento do super-resfriamento, mas também diminui a energia livre necessária para a sua formação. Para temperaturas suficientemente baixas, a nucleação pode ser desencadeada por alguns poucos átomos que se agregam formando uma partícula. O núcleo de tamanho crítico, neste caso, é reduzido. Portanto, é mais provável a nucleação para um grande super-resfriamento, pois o raio crítico é reduzido. A Figura 15.d apresenta o efeito do super-resfriamento no valor do raio crítico
aumenta muito o seu valor negativo à medida que a temperatura é reduzida. As Eqs. (15.7) e (15.8) indicam que não somente o raio crítico diminui com o aumento do super-resfriamento, mas também diminui a energia livre necessária para a sua formação. Para temperaturas suficientemente baixas, a nucleação pode ser desencadeada por alguns poucos átomos que se agregam formando uma partícula. O núcleo de tamanho crítico, neste caso, é reduzido. Portanto, é mais provável a nucleação para um grande super-resfriamento, pois o raio crítico é reduzido. A Figura 15.d apresenta o efeito do super-resfriamento no valor do raio crítico 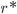 .
.
Figura 15.c – Variação de ∆G* e r* com a temperatura.
Figura 15.d – O efeito do super-resfriamento no valor do raio crítico r*.