O crescimento de grão é o processo pelo qual o tamanho médio de grão aumenta continuamente durante o tratamento térmico. Os grãos livres de deformação continuarão a crescer, se o material é deixado a uma temperatura elevada. Este crescimento não precisa ser precedido por processos de recuperação e recristalização. Ele ocorrerá, por exemplo, durante a sinterização (veja Capítulo 17, Sinterização) de uma cerâmica de grande utilização, como é o caso da alfa-alumina (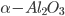 ) (1). Em temperaturas superiores a
) (1). Em temperaturas superiores a  , o crescimento exagerado dos grãos de alumina reduz muito a resistência mecânica da peça de cerâmica.
, o crescimento exagerado dos grãos de alumina reduz muito a resistência mecânica da peça de cerâmica.
A força motriz para o crescimento dos grãos é a redução da área superficial total do grão (veja Capítulo 12, Superfícies e Interfaces). Quando os grãos crescem em tamanho e decrescem em número, a área do contorno de grão diminui e, assim, a energia de superfície  decresce (2). Este é o fenômeno que faz com que as “células” presentes num filme bidimensional de espuma de sabão também cresçam em tamanho. Para isto as “células” de sabão coalescem com as células vizinhas. A Figura 16.j mostra, numa seqüencia de fotos, como as bolhas que apresentam um número pequeno de lados são absorvidas por bolhas maiores. Experiência semelhante foi realizada pelo metalurgista C. S. Smith (3), em 1953, para evidenciar as origens do processo. As “células” de sabão estão livres de alguns fatores que influenciam o crescimento de grãos no estado sólido, mas, como sugeriu Smith, pode ser considerado como um caso ideal de crescimento celular. A fim de explicar o crescimento de grãos no estado sólido, utilizaremos o modelo das células de uma espuma de sabão.
decresce (2). Este é o fenômeno que faz com que as “células” presentes num filme bidimensional de espuma de sabão também cresçam em tamanho. Para isto as “células” de sabão coalescem com as células vizinhas. A Figura 16.j mostra, numa seqüencia de fotos, como as bolhas que apresentam um número pequeno de lados são absorvidas por bolhas maiores. Experiência semelhante foi realizada pelo metalurgista C. S. Smith (3), em 1953, para evidenciar as origens do processo. As “células” de sabão estão livres de alguns fatores que influenciam o crescimento de grãos no estado sólido, mas, como sugeriu Smith, pode ser considerado como um caso ideal de crescimento celular. A fim de explicar o crescimento de grãos no estado sólido, utilizaremos o modelo das células de uma espuma de sabão.
Considere uma “célula” bidimensional de sabão, com pressão interna  , pressão externa
, pressão externa  , cuja interface possui espessura
, cuja interface possui espessura  (em que
(em que 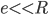 ), além de tensão superficial
), além de tensão superficial  . A Figura 16.j apresenta uma representação esquemática desta situação (4). Em uma espuma de sabão, composta de várias células, a curvatura da parede das células varia de célula para célula. Existe uma diferença de pressão em cada parede curva, e a pressão do lado côncavo será sempre maior que a do lado convexo, isto é
. A Figura 16.j apresenta uma representação esquemática desta situação (4). Em uma espuma de sabão, composta de várias células, a curvatura da parede das células varia de célula para célula. Existe uma diferença de pressão em cada parede curva, e a pressão do lado côncavo será sempre maior que a do lado convexo, isto é
 (16.3)
(16.3)
(multiplica-se por 2 porque o filme de sabão possui uma superfície interna e outra externa). A expressão 16.3 mostra que a diferença de pressão entre o interior e o exterior de um filme depende da tensão superficial  e do seu raio de curvatura. A difusão gasosa ocorrerá do lado de maior pressão para o lado de menor pressão e produz a movimentação do filme em sentido inverso, sempre no sentido do centro de curvatura.
e do seu raio de curvatura. A difusão gasosa ocorrerá do lado de maior pressão para o lado de menor pressão e produz a movimentação do filme em sentido inverso, sempre no sentido do centro de curvatura.
Este movimento do filme separando duas regiões pode ser comparado com o movimento dos contornos de grãos num sólido e consiste no fluxo viscoso de um grande número de planos atômicos e/ou na difusão de átomos individuais de um lado deste contorno de grão para o outro. A taxa de crescimento do grão será fixada pela taxa com que os átomos migram através do contorno de grão. Nem todos os grãos podem aumentar de tamanho, pois os grãos maiores crescem à custa dos menores até incorporá-los. A Figura 16.k apresenta uma representação esquemática do crescimento de grão por movimentação atômica através do contorno e a Figura 16.l é uma animação do crescimento dos grãos num material policristalino. Grãos com pequeno número de lados tendem a desaparecer enquanto grão com seis (hexágonos) ou mais número de lados tendem a crescer absorvendo os menores.
Figura 16.j – Seqüencia de fotos de bolhas de sabão: uma bolha com cinco lados é absorvida por uma bolha maior. Clique na seta para visualizar.
Figura 16.k – Movimento do contorno de grão.
Figura 16.l – Crescimento de grão: grãos com pequeno número de lados tendem a desaparecer enquanto grão com seis (hexágonos) ou mais número de lados tendem a crescer absorvendo os menores.