Considere-se que duas barras semi-infinitas, ambas de um mesmo metal puro A, sejam unidas pelas extremidades, e que entre elas há um depósito espesso de concentração 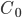 do metal puro B, soluto que irá se difundir para o interior das duas barras. Este sistema está representado na Figura 14.t num gráfico de concentração C da espécie em difusão (soluto) em função da distância x. A origem do sistema está localizada no centro do depósito espesso.
do metal puro B, soluto que irá se difundir para o interior das duas barras. Este sistema está representado na Figura 14.t num gráfico de concentração C da espécie em difusão (soluto) em função da distância x. A origem do sistema está localizada no centro do depósito espesso.
As seguintes condições de contorno ou hipóteses devem ser assumidas neste caso:
a- Para 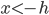 ou
ou 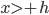 , tem-se que
, tem-se que 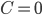 quando
quando 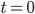 .
.
b- Para 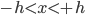 , tem-se que
, tem-se que 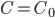 quando
quando 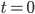 .
.
A aplicação das condições de contorno acima à Segunda Lei de Fick, Eq. (14.7), produz a seguinte solução:
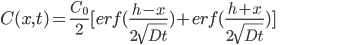 (14.31)
(14.31)
Figura 14.t – Variação da concentração de soluto com a distância x, para um sistema composto por duas barras semi-infinitas, ambas ricas no componente A, unidas entre si por um depósito espesso rico em componente B.