A literatura sobre Difusão no Estado Sólido considera que os experimentos realizados por Ernest Kirkendall (Tópico 14.10. O Efeito Kirkendall) na década de quarenta do século XX foram essenciais para o avanço da compreensão da difusão em sólidos. Kirkendall mostrou que ocorre interdifusão nos sólidos e que o mecanismo essencial para a migração é a existências de lacunas (também chamadas de vacâncias) nos sólidos.
Anteriormente ao trabalho de Kirkendall, o cientista japonês C. Matano, em 1933, já havia proposto uma técnica para a análise de dados experimentais de amostras de difusão. Esta técnica é fundamentada numa solução da equação 14.7 (Segunda Lei de Fick), que tinha sido proposta por L. Boltzmann (1) ainda no final do século XIX, em 1894. A solução de L. Boltzmann supõe que o coeficiente de difusão D seja função da concentração e do tempo. Para uma determinada composição, o coeficiente de difusão D pode também variar com a posição ao longo do material (x), se existir um gradiente de concentração nesse material. Isto requer a solução da Segunda Lei de Fick na forma:
 (14.34)
(14.34)
a solução para a equação (14.34) não é trivial, sendo normalmente empregada a integração gráfica para a determinação do coeficiente de difusão 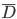 .
.
Considere-se o par de difusão semi-infinito (2), que se constitui de um bloco formado pela soldagem de duas ligas de composições diferentes, conforme mostra a Figura 14.x. No plano da solda são colocados vários fios de algum material que não se dissolve no sistema estudado. Estes fios são os marcadores no estudo do processo de difusão e, como foi discutido no Tópico 14.10, os marcadores mudam de posição durante o ensaio de difusão.
Após o ensaio de difusão e a análise química das fatias do material, o primeiro passo é traçar uma curva de concentração em função da distância ao longo da barra, medida a partir de um ponto de referência adequado (podendo ser, por exemplo, uma extremidade do par de difusão). Como segundo passo, deve-se escolher a seção transversal da barra na qual se igualam os fluxos totais das duas espécies atômicas que se difundem (A e B, por exemplo). Essa seção, conhecida como interface de Matano, encontra-se na posição em que as áreas M e N da Figura 14.x são iguais.
Uma vez localizada a interface de Matano (3), ela servirá agora de origem da coordenada x (as distâncias à direita da interface serão consideradas positivas e, à esquerda, consideradas negativas). A solução de Boltzmann para a Segunda Lei de Fick, para um sistema de coordenadas assim definido, será:
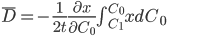 (14.35)
(14.35)
em que t é o tempo de difusão,  é a concentração em unidades atômicas a uma distância x da interface de Matano e
é a concentração em unidades atômicas a uma distância x da interface de Matano e  é a concentração de um lado do par de difusão, num ponto afastado da interface, em que a composição é constante e não é afetada pelo processo de difusão.
é a concentração de um lado do par de difusão, num ponto afastado da interface, em que a composição é constante e não é afetada pelo processo de difusão.
Figura 14.x – A interface de Matano num par de difusão semi-infinito.