Nomeiam-se de vias de alta difusividade as regiões em que a movimentação dos átomos é mais fácil. Como exemplo de vias de alta difusividade podemos citar os contornos de grão e a própria superfície do material. Os átomos podem se difundir mais rapidamente ao longo do contorno de grão do que no interior do material, no seu volume, por estarem submetidos a restrições menores nos contornos. Os contornos são regiões “ricas” em vazios e isto facilita o deslocamento dos átomos que se difundem. Do ponto de vista energético, a energia de ativação ( ) necessária para a difusão no contorno de grão é menor que aquela necessária para a difusão no volume.
) necessária para a difusão no contorno de grão é menor que aquela necessária para a difusão no volume.
Devido aos movimentos rápidos dos átomos nas superfícies livres, a difusão superficial desempenha um papel importante em processos metalúrgicos. A difusão em contorno de grão é de grande interesse porque, num metal policristalino, a soma das áreas dos contornos de grãos é, muitas vezes, maior do que a área das superfícies do corpo. Além disso, os contornos de grão formam uma rede por toda a amostra. Assim, quando medimos a difusão num metal policristalino, o resultado representa o efeito conjunto de difusão volumétrica ( ), pelo contorno de grão (
), pelo contorno de grão (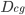 ) e pela superfície (
) e pela superfície ( ), isto é, obtemos um coeficiente de difusão aparente
), isto é, obtemos um coeficiente de difusão aparente 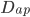 . Em geral, quanto menor o tamanho de grão, maior é a área dos contornos e maior é a importância dos contornos no processo.
. Em geral, quanto menor o tamanho de grão, maior é a área dos contornos e maior é a importância dos contornos no processo.
A equação de Difusão de tipo “Arrhenius” (equação 14.10) mostra que a difusividade depende da energia de ativação  e da temperatura
e da temperatura 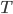 . Como se observou acima, nas curvas experimentais os efeitos da difusão volumétrica e em contornos de grão estão superpostos. No entanto, em temperaturas baixas (para que a difusão ocorra) o que define é a energia de ativação Q. Então, uma região de menor energia de ativação Q permitirá uma maior difusão de átomos, se comparada com outra que necessite de maiores valores de energia de ativação. Portanto, a difusão no contorno de grão predomina para baixas temperaturas. Para temperaturas mais elevadas há uma maior mobilidade dos átomos e a difusão volumétrica passa a ser predominante, pois a energia de ativação assume um caráter secundário.
. Como se observou acima, nas curvas experimentais os efeitos da difusão volumétrica e em contornos de grão estão superpostos. No entanto, em temperaturas baixas (para que a difusão ocorra) o que define é a energia de ativação Q. Então, uma região de menor energia de ativação Q permitirá uma maior difusão de átomos, se comparada com outra que necessite de maiores valores de energia de ativação. Portanto, a difusão no contorno de grão predomina para baixas temperaturas. Para temperaturas mais elevadas há uma maior mobilidade dos átomos e a difusão volumétrica passa a ser predominante, pois a energia de ativação assume um caráter secundário.
A Figura 14.z apresenta um gráfico de 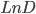 em função do inverso da temperatura absoluta (
em função do inverso da temperatura absoluta ( ) e mostra as regiões de predomínio da difusão volumétrica e de predomínio da difusão pelos contornos de grão.
) e mostra as regiões de predomínio da difusão volumétrica e de predomínio da difusão pelos contornos de grão.
Figura 14.y – Perfil de concentração para difusão em contorno de grão.
Figura 14.z – Gráfico de  em função do inverso da temperatura absoluta (
em função do inverso da temperatura absoluta (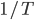 ), mostrando as regiões de predomínio da difusão volumétrica e de predomínio da difusão pelos contornos de grão.
), mostrando as regiões de predomínio da difusão volumétrica e de predomínio da difusão pelos contornos de grão.