São apresentadas a seguir as equações fundamentais obtidas a partir de considerações sobre um modelo de nucleação e crescimento de núcleos esféricos dentro de um líquido. Considera-se que a nucleação é homogênea, isto é, não existem sítios preferenciais para a ocorrência dos núcleos.
Seja V o volume de uma partícula e S sua área superficial. A variação total de energia livre, associada à formação de uma partícula de raio r, 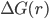 , é:
, é:
 (15.1)
(15.1)
onde 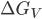 é a variação da energia livre por unidade de volume solidificado e
é a variação da energia livre por unidade de volume solidificado e 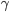 é a energia superficial ou energia por unidade de área. Como a partícula é esférica e de raio r, tem-se que
é a energia superficial ou energia por unidade de área. Como a partícula é esférica e de raio r, tem-se que 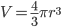 e
e 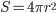 . Então:
. Então:
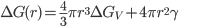 (15.2)
(15.2)
Cada termo desta equação está representado na Figura 15.b, que mostra a variação de 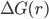 com o raio de uma partícula sólida.
com o raio de uma partícula sólida.
Também na Figura 15.b pode-se ver que 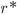 é um ponto de máximo (1) da Eq. (15.2) e que
é um ponto de máximo (1) da Eq. (15.2) e que 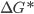 é a ordenada correspondente. A substituição novamente na Eq. (15.2) do máximo obtido produz
é a ordenada correspondente. A substituição novamente na Eq. (15.2) do máximo obtido produz  . As equações obtidas são:
. As equações obtidas são:
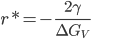 (15.3)
(15.3)
e
 (15.4)
(15.4)
O raio  é chamado raio crítico ou raio do núcleo de tamanho crítico. Partículas com
é chamado raio crítico ou raio do núcleo de tamanho crítico. Partículas com 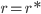 são chamadas núcleos críticos ou núcleos de tamanho crítico. Partículas com
são chamadas núcleos críticos ou núcleos de tamanho crítico. Partículas com  , são chamadas embriões; partículas com
, são chamadas embriões; partículas com 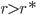 , são chamadas núcleos. As partículas do raio maior que
, são chamadas núcleos. As partículas do raio maior que 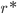 diminuirão sua energia livre por meio do seu crescimento através da adesão de átomos (ou moléculas); as partículas de raio menor que
diminuirão sua energia livre por meio do seu crescimento através da adesão de átomos (ou moléculas); as partículas de raio menor que 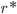 , para diminuir a energia livre, tenderão a se dissolver porque átomos (ou moléculas) migrarão para fora da partícula, retornando a matriz líquida. Partículas com
, para diminuir a energia livre, tenderão a se dissolver porque átomos (ou moléculas) migrarão para fora da partícula, retornando a matriz líquida. Partículas com  poderão crescer ou dissolver-se, pois ambos os processos produzirão a diminuição da energia livre. A quantidade
poderão crescer ou dissolver-se, pois ambos os processos produzirão a diminuição da energia livre. A quantidade  representa a barreira energética associada à formação de um núcleo de tamanho crítico.
representa a barreira energética associada à formação de um núcleo de tamanho crítico.
Figura 15.b – Nucleação de núcleos sólidos e esféricos a partir de um líquido puro.