Na teoria de nucleação homogênea, formulada por Volmer e Weber (1) em 1926, admite-se que o núcleo estável é resultante da adição sucessiva de átomos individuais ao embrião, sendo a reação unidirecional com sentido matriz -> embrião. Em conseqüência, novos átomos devem ser adicionados ao ponto onde ocorre a reação, para compensar os que dali foram removidos. Pelo modelo proposto isto não afetaria a presença de um virtual equilíbrio existente no sistema, pois admite-se que o número de núcleos n é pequeno quando comparado com N, número total de átomos do sistema estudado. Nesta teoria desconsidera-se a reação reversa, ou seja, uma vez que o átomo saltou para o embrião, ele não retornará à matriz e assume-se que o processo de crescimento é tão lento que torna possível considerar o número de agrupamentos de raio crítico n* como sendo o número de equilíbrio. Nesta situação, o número de núcleos da nova fase com raio crítico é dado pela seguinte equação:
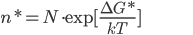 (15.9)
(15.9)
em que n* é o número de núcleos; N é o número total de átomos ou de unidades moleculares; k é a constante de Boltzmann (2) e T é a temperatura em graus Kelvin (K).
O cálculo da velocidade de nucleação I resulta da multiplicação de n* pela taxa de crescimento dos núcleos de raio crítico. Esta segunda quantidade (3) é fornecida pela seguinte equação:
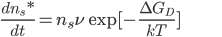 (15.10)
(15.10)
em que 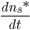 é a taxa de crescimento dos núcleos de raio crítico;
é a taxa de crescimento dos núcleos de raio crítico; 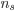 é o número de átomos que atravessam a interface por segundo; k é a constante de Boltzmann; T é a temperatura absoluta;
é o número de átomos que atravessam a interface por segundo; k é a constante de Boltzmann; T é a temperatura absoluta; 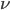 é a freqüência de vibração atômica e vale kT/h, onde h é a constante de Planck (4);
é a freqüência de vibração atômica e vale kT/h, onde h é a constante de Planck (4); 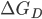 é a energia livre de ativação para mover os átomos adjacentes à interface criada.
é a energia livre de ativação para mover os átomos adjacentes à interface criada.
Multiplicando-se as equações 15.9 e (15.10) teremos:
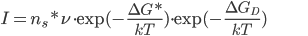
 (15.11)
(15.11)
em que I é a velocidade de nucleação e 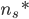 é o valor de
é o valor de 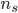 quando os embriões possuem o raio crítico,
quando os embriões possuem o raio crítico, 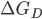 é a energia livre de ativação para mover os átomos adjacentes à interface criada e
é a energia livre de ativação para mover os átomos adjacentes à interface criada e 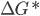 é dado pela equação (15.8) do item anterior.
é dado pela equação (15.8) do item anterior.
Outros teóricos já propuseram modificações nesta teoria (1). Apesar da introdução de modelos físicos mais consistentes, essas revisões propostas atuam exclusivamente sobre o fator pré-exponencial de equação (15.11). Nos intervalos onde usualmente ocorre a nucleação, todavia, a variação devido ao fator  é muito menor que a variação devido ao termo exponencial
é muito menor que a variação devido ao termo exponencial 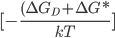 . Além disto, a precisão nas determinações experimentais da velocidade de nucleação não é grande tornando possível considerar a equação (15.11) como adequada. A Figura 15.e apresenta num gráfico a variação da velocidade de nucleação com a temperatura.
. Além disto, a precisão nas determinações experimentais da velocidade de nucleação não é grande tornando possível considerar a equação (15.11) como adequada. A Figura 15.e apresenta num gráfico a variação da velocidade de nucleação com a temperatura.
Utilizando as equações 15.6 e 15.8 do Tópico anterior em conjunto com a equação 15.11, observamos que, quando 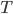 for um valor próximo de
for um valor próximo de  ,
, 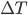 tende para zero, e a primeira exponencial dentro da Equação 15.11 torna-se nula. Isso implica que na temperatura de fusão a velocidade de nucleação deve ser nula. À medida que a temperatura decresce,
tende para zero, e a primeira exponencial dentro da Equação 15.11 torna-se nula. Isso implica que na temperatura de fusão a velocidade de nucleação deve ser nula. À medida que a temperatura decresce, 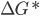 cai violentamente e a velocidade de nucleação aumenta. Entretanto,
cai violentamente e a velocidade de nucleação aumenta. Entretanto, 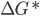 torna-se logo desprezível comparado com
torna-se logo desprezível comparado com 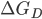 ,
, 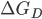 domina então a Equação 15.11, e N decresce com a temperatura. Conseqüentemente, há um máximo na velocidade de nucleação homogênea, que pode estar localizado consideravelmente abaixo do ponto de fusão
domina então a Equação 15.11, e N decresce com a temperatura. Conseqüentemente, há um máximo na velocidade de nucleação homogênea, que pode estar localizado consideravelmente abaixo do ponto de fusão . À medida que a temperatura decresce, a velocidade de nucleação passa a ser controlada pela difusão, isto é, pela velocidade de salto dos átomos pela interface entre o líquido o sólido.
. À medida que a temperatura decresce, a velocidade de nucleação passa a ser controlada pela difusão, isto é, pela velocidade de salto dos átomos pela interface entre o líquido o sólido.
A Tab. 15.1 (5) apresenta valores experimentais de super-resfriamento de diferentes materiais que se solidificaram a partir do estado líquido. Nesta tabela,  é a mais baixa temperatura na qual um líquido pode ser super-resfriado sem cristalizar-se e
é a mais baixa temperatura na qual um líquido pode ser super-resfriado sem cristalizar-se e  . O máximo super-resfriamento conseguido para estas substâncias é entre 13% e 26% menor que o valor da temperatura de fusão destes materiais.
. O máximo super-resfriamento conseguido para estas substâncias é entre 13% e 26% menor que o valor da temperatura de fusão destes materiais.
Tab. 15.1. Temperaturas de super-resfriamentos para diferentes metais e substâncias (5)
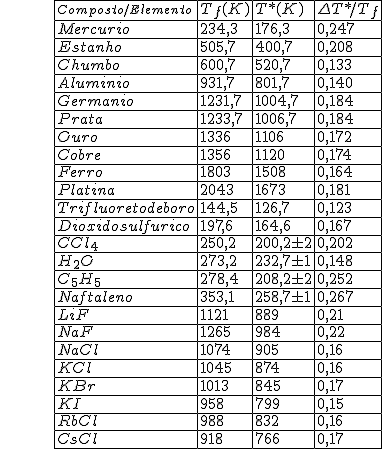
Figura 15.e – A variação da velocidade de nucleação com a temperatura.